Angle Puzzles Challenge Set: Solving for Missing Angle Measures Using Geometry Theorems
Students solve to find missing angle measures, using algebra and geometry skills together for these challenge puzzles. This puzzle pack includes three sets.
OVERVIEW of the 3 sets included:
- Parallel Lines & Transversals (2 versions included for easy differentiation)
- Triangle Theorems & Properties (4 puzzles included at different difficulty levels)
- Circle Theorems (4 puzzles included with a range of difficulty levels)
__________________________________________________________________________________
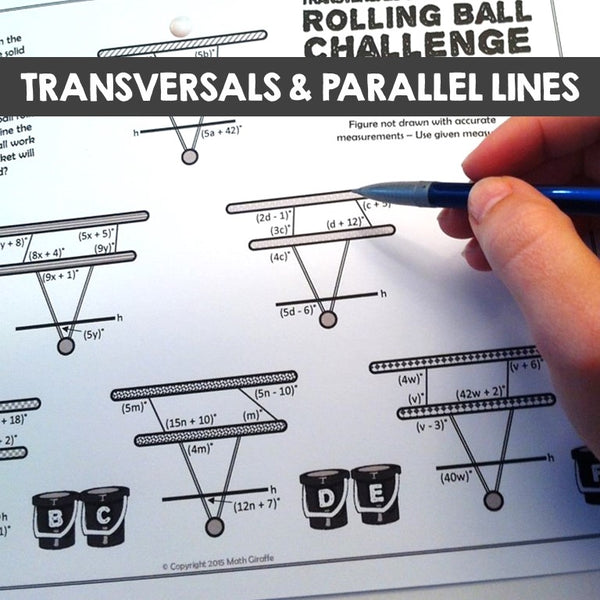
More about Set #1 - Parallel Lines and Transversals
Using properties and theorems for parallel lines cut by a transversal, students write and solve systems of equations to determine angle measures.
The goal is to figure out the slight slant of each set of ledges in order to determine which way the ball will roll. Students have to figure out where the ball will end up. This activity combines Geometry skills, Algebra skills, and Critical Thinking skills.
There are 2 versions of the worksheet for easy differentiation. You can use both on different days, choose one, or use some of each to differentiate by ability.
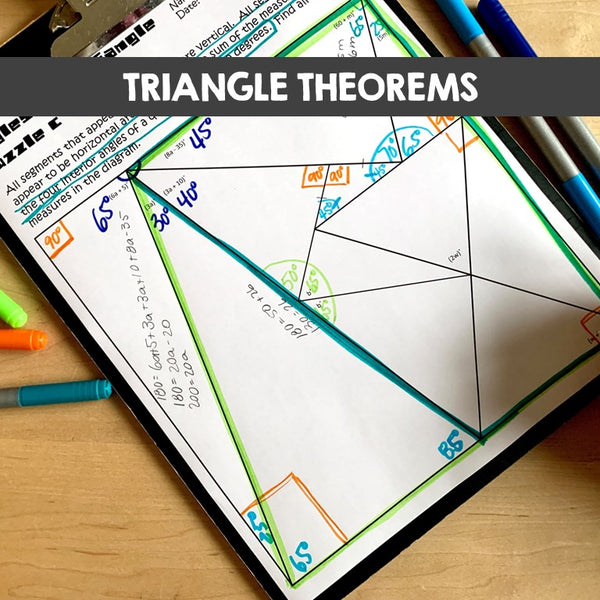
More about Set #2 - Triangles
Solving for Missing Angles Using Properties of Triangles: Challenge Puzzles for Triangle Theorems
This set of four puzzles offers a challenge to students learning about angles in a triangle. The puzzles include algebra applications. Students must set up and solve linear equations to find some of the missing angle measures. The puzzles will really get your students thinking about how to get from one part of a diagram to another. Each puzzle uses sets of different skills with triangles and angles. You can use all four at once or set them up as learning stations. Students can progress from the easiest (Puzzle D) to the most difficult (Puzzle C) or you can use the different puzzles to differentiate in your classroom.
Prior Knowledge Required:
- Solving linear equations
- Base angles of an isosceles triangle are congruent.
- Vertical angles are congruent.
- The sum of angle measures in a triangle is 180 degrees.
- The sum of angle measures that form a straight angle is 180 degrees.
- Alternate interior angles are congruent.
- Definition of rectangle
- Definition of congruent triangles
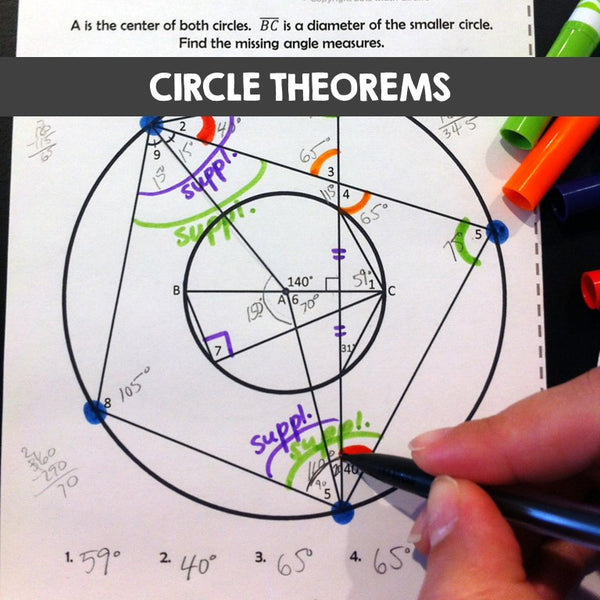
More about Set #3 - Circles
Circle Theorems & Properties of Angles in Circles - Practice / Review:
4 half sheet angle puzzles of varying difficulty plus answer keys
Puzzle #1 is the most difficult (VERY CHALLENGING – BEWARE!) and #4 is the most basic. Use puzzles 1 and 2 as challenges and 3 and 4 as homework or warm-ups, or distribute to specific students to differentiate. These make great partner activities or stations as well.
The puzzles cover a range of difficulty levels.
Students will use a variety of theorems to find each missing angle measure.
Circle Theorems:
- A chord that is perpendicular to the diameter is bisected by the diameter.
- An inscribed angle’s measure is half of the central angle’s measure.
- Inscribed angles subtended by the same arc (or on the same chord) are congruent.
- An inscribed angle in a semicircle (or on the diameter) is a right angle.
- Opposite angles in an inscribed (or cyclic) quadrilateral are supplementary.
- The lengths of two tangents from a point to the circle are always equal.
Basics Properties of Circles:
- All radii are congruent.
- A tangent to a circle meets the radius at a right angle.
Prior Knowledge Required:
- Triangle Sum Theorem (180 degrees)
- Interior Angles of a Quadrilateral Theorem (360 degrees)
- Vertical Angles Theorem (congruent)
- Base Angles of an Isosceles Triangle Theorem (congruent)